评价类模型——层次分析法AHP
Updated on: 2024-02-26 14:34:29
一、层次分析法(原理)
1.权重表
各指标和为1、某指标下各对象和为1
2.指标/目标对象的确定(检索)
尽量有据可依专业性强,即检索文献、虫部落检索网站:Google、百度、知网、万方、微信、知乎等
3.权重确定(层次分析思想)
①两两对比进行评分, 并作出对应比较矩阵(判断矩阵)
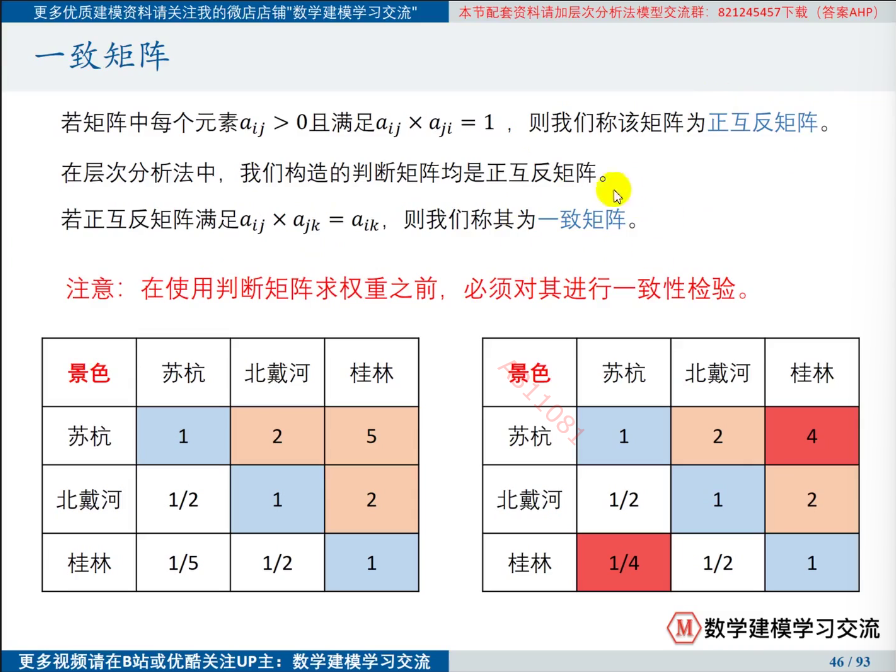
需要注意的是,一直矩阵各行或者各列表现出等比例,在一致性检验不合格时应当向等比例方向进行修改。
进行评分时应当由专家群体进行评分,但往往实际上在建模过程中自己评。
②进行判断矩阵的一致性检验
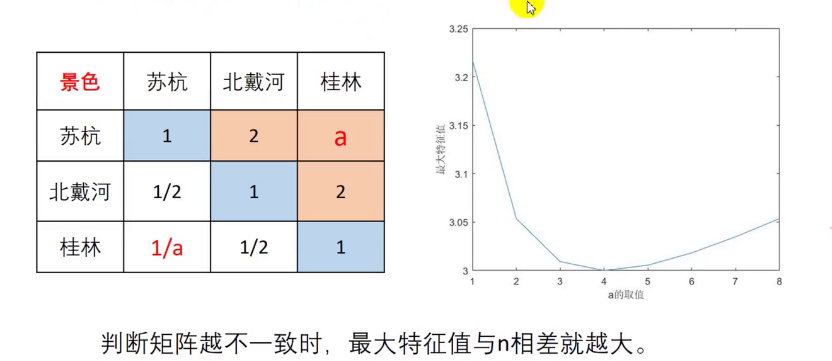
一致性检验的步骤如下:
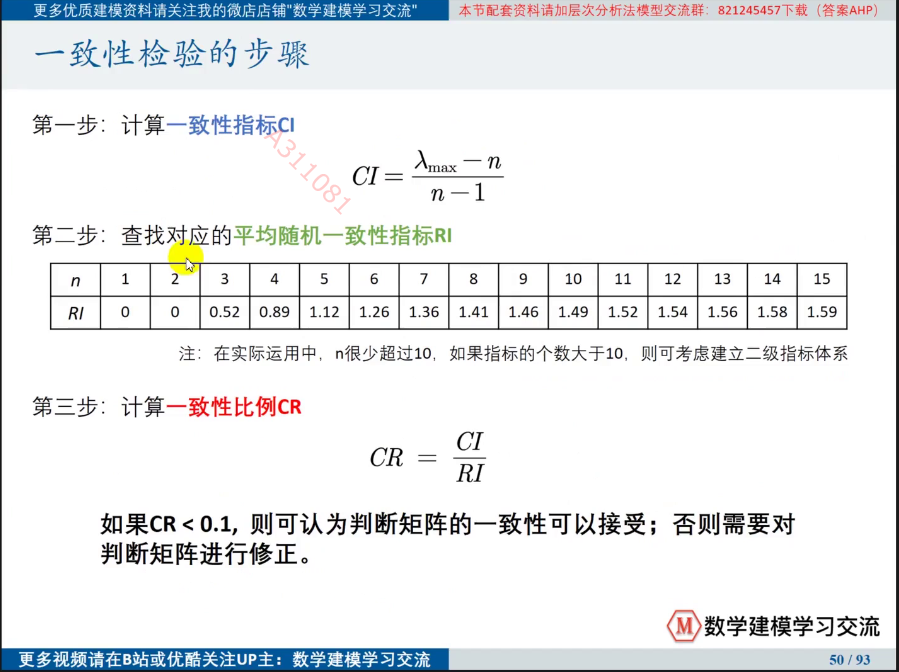
③权重计算方法
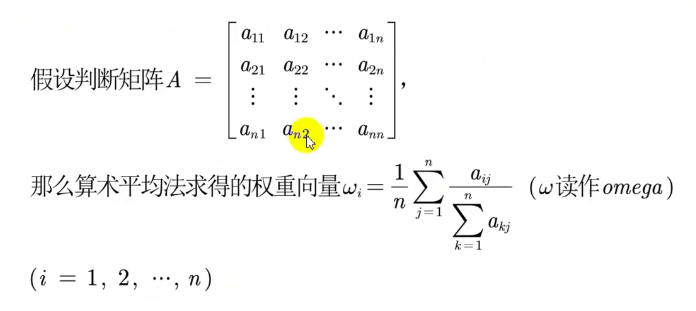
A.算术平均数法
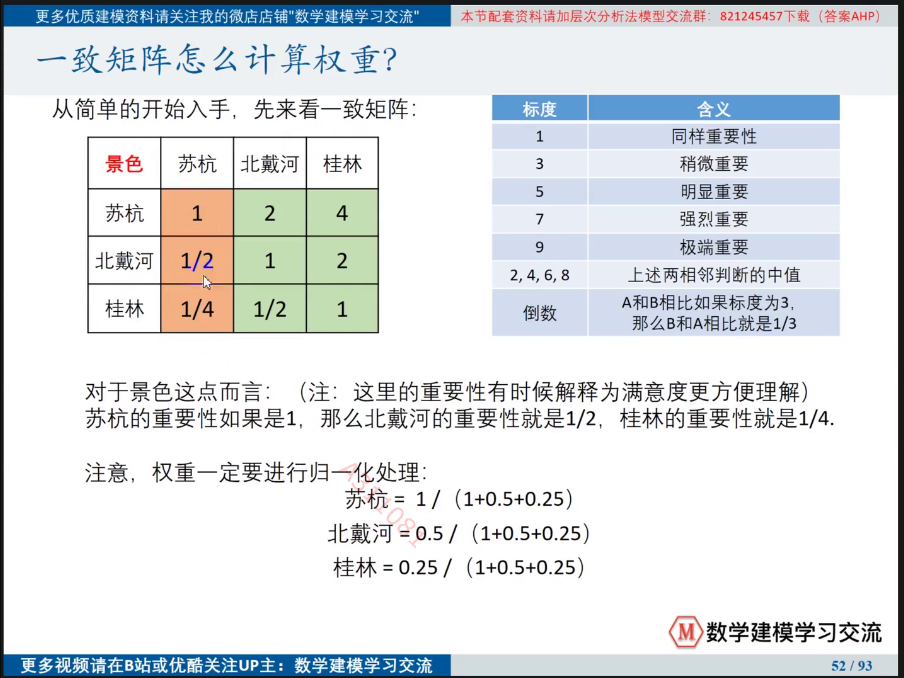
a.对于一致方阵
进行归一化处理后,对用**第一列各元素÷第一列所有元素求和**,这是由于各行各列成比例,信息相等。
b.非一致方阵
由于各行或各列不成比例,信息不完全相同,因此应当充分利用所有列或行信息。
(某对象(行名)第一列权重+第二列权重+第三列权重)/ 列数(因每列和都为1)

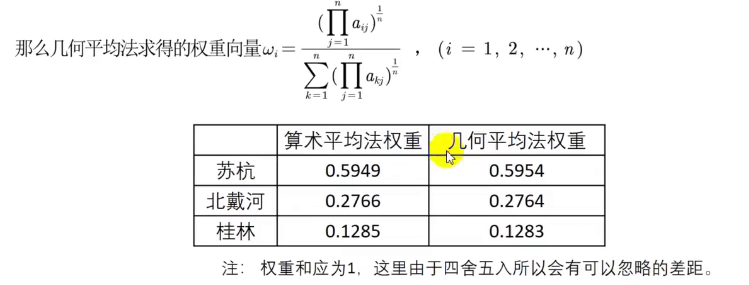
B.几何平均数法

C.特征值法
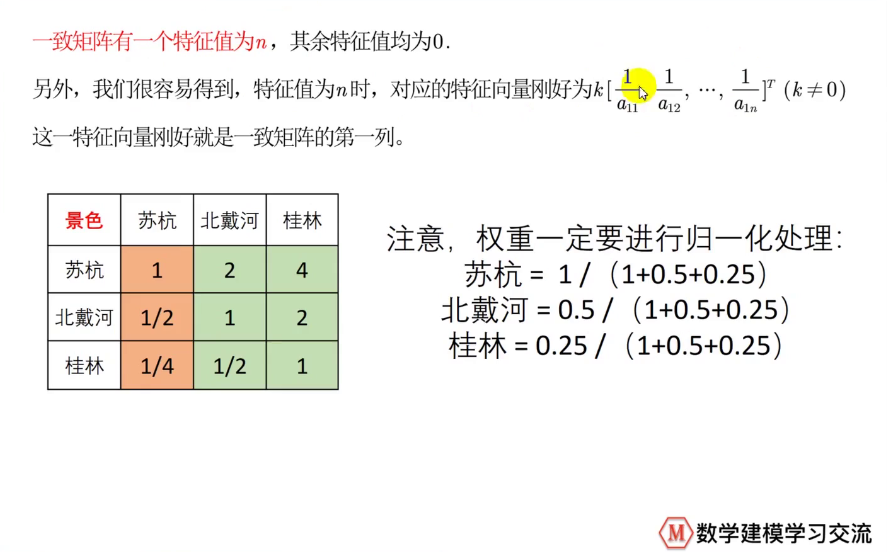
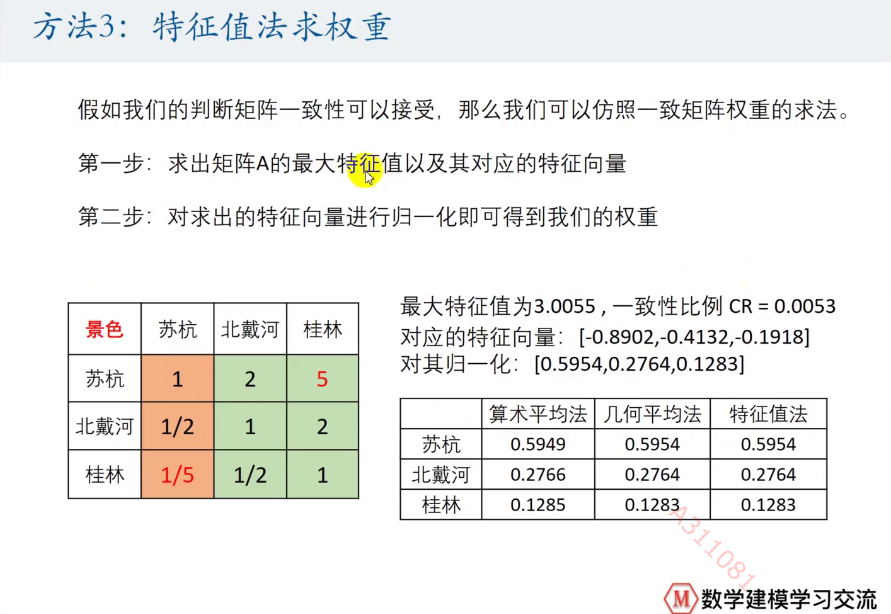
④计算最终得分
将每列各指标权重与各对象权重进行相乘后相加。
二、层次分析法代码
# 导入相关库
import numpy as np
# index = np.mat([0.2, 0.3, 0.5],["对象1","对象2","对象3"]) # 每一行代表一个对象的指标权重
# A为自己构造的输入判别矩阵(按行输入)
A = np.array([[1, 1 / 2, 4, 3, 3],
[2, 1, 7, 5, 5],
[1 / 5, 1 / 7, 1, 1 / 2, 1 / 3],
[1 / 3, 1 / 5, 2, 1, 1],
[1 / 3, 1 / 5, 3, 1, 1]])
# 查看行数和列数
[m, n] = A.shape
B = np.zeros((m, n))
# 求特征值和特征向量
V, D = np.linalg.eig(A)
print('特征值:')
print(V)
print('特征向量:')
print(D, "\n", "_" * 50)
# 最大特征值
tzz = np.max(V)
# print(tzz)
# 对应最大特征向量
k = [i for i in range(len(V)) if V[i] == np.max(V)]
tzx = D[:, k]
# print(tzx)
# 一致性检验
CI = (tzz - n) / (n - 1)
RI = [0, 0, 0.52, 0.89, 1.12, 1.26, 1.36, 1.41, 1.46, 1.49, 1.52, 1.54, 1.56, 1.58, 1.59]
# 判断是否通过一致性检验
CR = CI / RI[n]
print('CI=', CI, "\n", 'CR=', CR, "\n")
if CR >= 0.1:
print('没有通过一致性检验\n')
else:
print('通过一致性检验', "\n", "_" * 50)
# 算术平均数权重
C = np.zeros((n, 1))
for i in range(n):
B[:, i] = A[:, i] / np.sum(A, axis=0)[i]
for i in range(n):
C[i] = np.sum(B[i, :]) / n
print("算术平均数法权重", "\n", C, "\n", "_" * 50)
# 几何平均数权重
C1 = np.zeros((n, 1))
for i in range(n):
C1[i] = np.prod(A[i, :]) ** (1 / float(n))
geo_mean_sum = np.sum(C1)
for i in range(n):
C1[i] = C1[i] / geo_mean_sum
print("几何平均数法权重", "\n", C1, "\n", "_" * 50)
# 特征向量法
quan = np.zeros((n, 1))
for i in range(0, n):
quan[i] = tzx[i] / np.sum(tzx)
Q = quan
print("特征向量法权重", "\n", Q, "\n", "_" * 50)
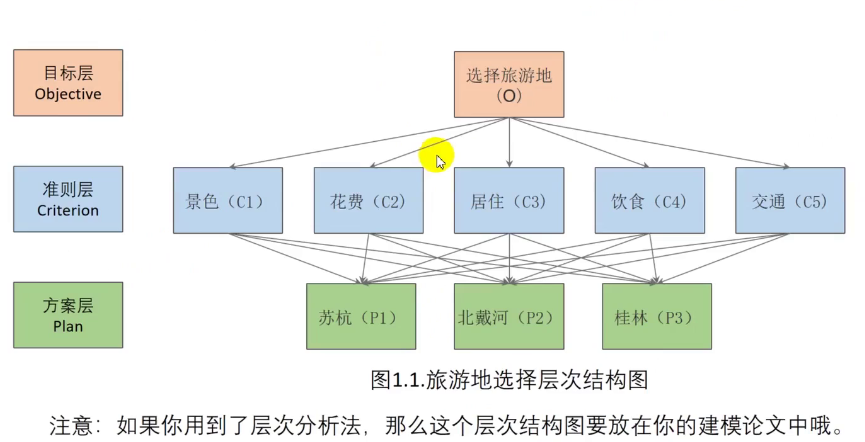
三、层次分析法论文书写与层次结构图